Takeaway points
  • Load carrying capacity increases with σy and decreases with E.
  • Load carrying capacity grows in proportion to diameter square. (Assuming L=kD)
  • Nested concave surfaces have a much increased load carrying capacity.
Formulas for Herzian Contact

In order to achieve independence from small geometrical imperfections in their mating elements, kinematic mounts use Herzian contact geometries, where the contact area between the mating elements starts out as zero (point or line contact) and grows as a function of the applied force due to the elastic propeties of the material.

This contact area growth process has the advantage that it geometriaclly averages small imperfections, thereby reducing the mount's sensitivty to them.

The equations used below are quoted from Roark's Formulas for Stress and Strain, Warren C. Young and Richard Budynas, sixth edition (1989), and rearanged slightly. (Chapter 13, Table 33, page 650)

These equation are empirical, but largely agree with results optained from FEA studies we performed, and with measured deformations.

The basic equations for elastic point and line contact stresses are listed below. (Numberic subscripts apply when the two contacting materials are not the same)

Notations and Parameters:
Elastic modulus:E
Shear modulus:G
Poisson's Ratio:ν = E/2G - 1
Yield stress:σy
Applied force:F
Diameter:D
Length:L
 Sphere-PlaneCylinder-Plane
Elastic ConstantCE = (1-ν12)/E1 + (1-ν22)/E2 = 2·(1-ν2)/E
Contact Diameter/Widthb = 1.44·[F CE D]1/3b = 1.60·[F CE D/L]1/2
Contact AreaA = πb2/4A = b·L 
Deformationx = 0.5·(b2/D)x = 0.124·(b2/D)·ln(2.791·D/b)
Maximum Stressσ = 1.5·F/Aσ = 1.277·F/A
Load LimitFmax = (σy/0.918)3(D2CE2)Fmax = (σy/0.798)2(LDCE)

When calculating kinematic mount elements, a few straight forward adaptations are necessary: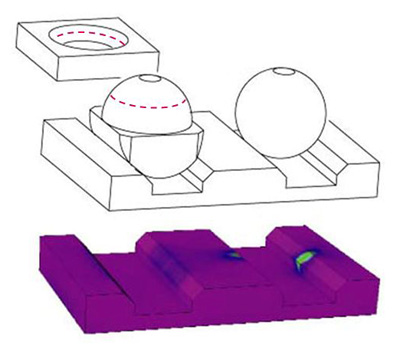

  • For cylinder-in-V-grooves mating elements, there are 2 lines of contact, but only the vertical component of the contact force goes towards supporting the load.
  • For sphere-in-cone mating elements, the effective contact is that of a cylinder-to-a-plane, with the cylinder having the same diameter as the sphere, and a length equal to the circumference of the line of contact. As with the V-groove, only the vertical component of the force goes towards supporting the load.
  • In the case of a rounded V-groove or cone ("Roman arc" cross-section) the effective diameter of the contact is Deff = D1·D2/(D1-D2).

An interesting effect in elastic contacts is that the maximum stress points occur not at the mating surfaces, but rather deeper inside the bodies.