It is easiest to illustrate kinematicity by way of a two-dimensional example, in which a beam (purple) is attached to the factory floor using two mating elements (Orange).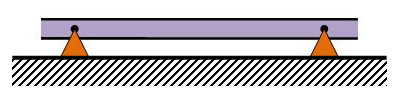

Over-constrained. The two pin joints "fight each other" over the horizontal positioning of the beam.

In the simplest configuration, the two mating elements are pin joints that are rigidly attached to the floor. Each pin joint determines the position of its end of the beam in X and Y, but allows the beam to rotate (theta).

Overall, therefore, the two mating elements together constrain 2+2=4 degrees of freedom, while the beam (in the plane) has only 3 degrees of freedom. Since 4>3, this situation is over constrained.

The practical implications in this case are:

• Any manufactuing/assembly mismatch between the distance between the pin blocks (as assembled on the factory floor) and the two pin holes punched in the beam will cause very large stresses in the assembly (if the pins can even be inserted at all).
• The pin holes can be enlarged to accomodate the tolerance in the position of the pin joints, but then the pins will be loose, and we'll end up in an under-constrained situation.
• If the beam expands due to a temperature change (for example), large compressive stresses will develop inside of it.
• Since the horizontal position of the beam is determined by the result of the "fight" between the two pin joints, it is not really well knows, and can change over time or across multiple assembly operations.

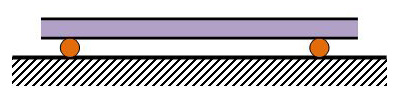
Under-constrained. The beam can still move in the horizontal direction.

In a second configuration the two mating elements are roller pins. Each roller pin only determines the position of its end of the beam in the Y direction, and allows the beam to move freely in the X direction and to rotate in the plane.

Overall, the two mating elements now constrain only 1+1=2 degrees of freedom, while the beam still has 3 degrees of freedom in the plane, Since 2<3, this situation is under-constrained.

The practical implications in this case are quite simple:

The the beam is not supported in the X direction and so can move freely - its position is not known, and it cannot exert any counter-forces in that direction.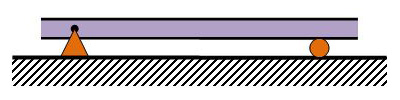

Well-constrained. 3 constrains for 3 degrees-of-freedom (X-Y-θ)

The kinematic mount aims to have exctly 3 constrains for the 3 degrees of freedom. We do this here by using one pin joint mating element (constraining two degrees of freemdom), and one roller pin mating element (constraining only one).

overall, exactly 2+1=3 degrees of freedom are constrained, and so the set of equations governing the beam is well posed.

The benefits of such a mount are:

• There is no requirement that either the pin blocks or the pin holes be placed with high tolerance.
• The beam is never over-constrained and so is never stressed due to being assembled.
• Repeatable assemblies place the beam in the same position.
• The positioning of the beam is rigid.

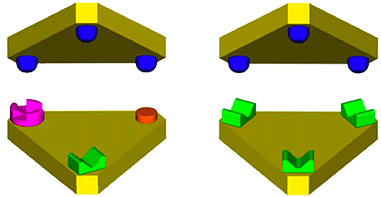
Similar reasoning can be applied in the 3D world of solid objects, where there are a total of 6 degrees of freedom for each body (Motion along the X,Y and Z axes, and rotation about each of them).

Kinematic solutions in 3D exist, and include (among many) the cone-v-flat mount and the 3-groove mount. Both of these mounts are kinematic, since they constrain a total of exactly 6 degrees of freedom. The Three Groove Mount is more elegant, it is symmetrical, and it is the basis for our family of three-legged kinematic mounts.

3-2-1 mount "cone-v-flat"	2-2-2 mount "3-groove mount"
(images courtesy of Ms. Outlier)

The products we offer are used to create 3-D kinematic mounts, while also addressing issues such as fragility and low load-carrying capcity that are usually inherent to kinematic mount designs.

For more information, see our technology pages.